The first person is 100 cm tall.
Each subsequent person is 20% taller than the person before.
What will be the height of the fifth person?
The first person is 100 cm tall.
Each subsequent person is 20% taller than the person before.
What will be the height of the fifth person?
Make two fractions with all the digits from 0 to 9.
Use each digit once.
They add up to exactly 1.
What is one of the fractions?
Savin's problem:
Using each of the digits 1,2,3, and 4 twice, write out an eight-digit number in which there is one digit between the ones, two digits between the twos, three digits between the threes, and four digits between the fours.
How many such numbers?
What is the sum of the first 100 prime numbers?
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself.
The average of 99 consecutive numbers is 99.
What is the average of the nine smallest of these numbers?
The natural numbers are the counting numbers, like 1, 2, 3, et cetera.
An even number is a natural number which is "evenly divisible" by two.
An odd number is a natural number which is not a multiple of two.
Which statement is correct?
A magic square is an arrangement of integers, in a square grid, where the numbers in each row, and in each column, and the numbers in the diagonals, all add up to the same number.
Place numbers 13, 14, 15, and 16 in the square to make a magic square.
Which number do you place in the top left cell?
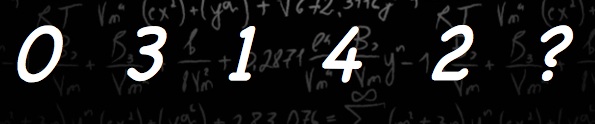Leslie Green asks:
What is the next number in the sequence?
0, 3, 1, 4, 2
(NOTE: It is a single sequence and not two sequences interleaved.)
Shakuntala Devi was undoubtedly the most brilliant arithmetic mental calculator of all time. In 1977 she mentally calculated the 23rd root of a 201 digit number in a mere 50 seconds. She toured the world showing how she could do calculations faster than they could be entered into and solved by the computers of the day.
The problem for you is much simpler: Evaluate (without using a calculator) the 20th root of the 11 digit number consisting of 1 followed by all zeros.
Author: Leslie Green
The numbers
129
CXXIX
10000001
81
all have the same value.
Why is CXXIX the odd one out?
Author: Leslie Green
Present 100 as a sum of positive integers such that their product is at its maximum value.
How many numbers do you use?
The last digit of the number 777 is 
Find the hundreds digit (third digit from the right) of the product: 
Which gives the largest answer?
Which is the letter D in the row?
What number is 3 greater than 11?
Which is the sum of all digits of the decimal representation of 516 x 165?
Which gives the largest answer?
If you wrote all the whole numbers from 1 through 1000, how many times would you write the digit 4?
With a 1 after a nine-digit number, it is the same as a 1 before it. 
I multiply the two page numbers and get 6162. 
If XY = 1024 and both numbers are integers, which of the following could not be a value of X nor Y?
0.999 . . . means infinitely repeating decimals.