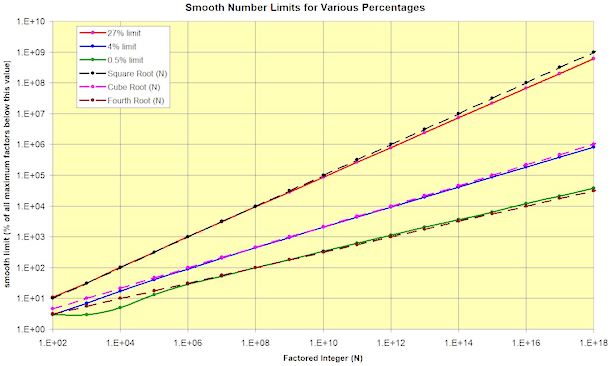
 'Smooth numbers' are those that factor easily in the sense that all their prime factors are lower than some specified limit. If we take a block of consecutive integers, it is obvious that half will be divisible by 2, one third will be divisible by 3, and so on. But the question "How many will not have a prime factor above the square root of the number being tested?" is somewhat more difficult. This graph answers such questions.
'Smooth numbers' are those that factor easily in the sense that all their prime factors are lower than some specified limit. If we take a block of consecutive integers, it is obvious that half will be divisible by 2, one third will be divisible by 3, and so on. But the question "How many will not have a prime factor above the square root of the number being tested?" is somewhat more difficult. This graph answers such questions.
If you consider integers in the region of 1E8 (100 million), around 27% of them will not have a prime factor larger than 1E4 (10,000).
The question for you is this: If you consider random integers around 1E18, what percentage of them will not have a prime factor exceeding 1,000,000?
by Leslie Green